不多说,直接上干货!
前言
一种最终一致的算法,paxos算法。
paxos算法是由大牛lamport发明的,关于paxos算法有很多趣事。比如lamport论文最初由故事描述来引入算法,以至于那班习惯数学公式的评委将该论文打回,导致该论文延误了8年才公开发表。另外,google的chubby的作者Mike Burrows说过,世界上只有一种一致性算法,那就是paxos。
两将军问题
为了引入该算法,首先提出一种场景,即两将军问题:
有两支军队,它们分别有一位将军领导,现在准备攻击一座修筑了防御工事的城市。这两支军队都驻扎在那座城市的附近,分占一座山头。一道山谷把两座山分隔开来,并且两位将军唯一的通信方式就是派各自的信使来往于山谷两边。不幸的是,这个山谷已经被那座城市的保卫者占领,并且存在一种可能,那就是任何被派出的信使通过山谷是会被捕。 请注意,虽然两位将军已经就攻击那座城市达成共识,但在他们各自占领山头阵地之前,并没有就进攻时间达成共识。两位将军必须让自己的军队同时进攻城市才能取得成功。因此,他们必须互相沟通,以确定一个时间来攻击,并同意就在那时攻击。如果只有一个将军进行攻击,那么这将是一个灾难性的失败。
两将军问题本质上就是通信被篡改时能否解决一致性问题。这个问题已经被很多人证明不能。(见文献1)。因而由此推及的拜占庭将军问题(多将军问题)也同样不能被解决。
PAXOS算法
一个叫做Paxos的希腊城邦,这个岛按照议会民主制的政治模式制订法律,但是没有人愿意将自己的全部时间和精力放在这种事情上。所以无论是议员,议长或者传递纸条的服务员都不能承诺别人需要时一定会出现,也无法承诺批准决议或者传递消息的时间。但是这里假设没有拜占庭将军问题(Byzantine failure,即虽然有可能一个消息被传递了两次,但是绝对不会出现错误的消息);只要等待足够的时间,消息就会被传到。另外,Paxos岛上的议员是不会反对其他议员提出的决议的。
这里不再赘述算法的推导及证明过程,这里简单描述下算法理解。
基本思想也是两阶段提交。但是与两阶段目的不同。
1. 第一阶段主要目的是选出提案编号最大的proposer。
其描述如下,所有的proposer向超过半数的acceptor提出编号为n的提案,acceptor收到编号为n的请求,会出现两种情况
a. 编号n大于所有acceptor之前已经批准过的proposal的最大编号及内容m。acceptor同意该proposal,响应[n, m]回proposer,并且承诺今后不再批准任何编号小于n的提案。
b. 编号n小于acceptor之前批准过的任意proposal的编号。acceptor拒绝该proposal。
2. 第二阶段尝试对某一proposal达成一致。
proposer收到超过半数的acceptor返回的响应,proposer就会将响应的最大编号[n, m]对应的提案提交到acceptor要求acceptor批准该提案。acceptor收到最大编号[n, m]的提案,也分为两种情况
a. 未响应过编号大于n的prepare请求。通过该提案。
b. 已响应过编号大于n的prepare请求。拒绝该提案。
整个算法表面上并不难理解,难在实现细节的难易程度和各种异常情况的推导及考虑。如果对上述算法有理解困难的,参考文献4和文献5的例子,其中文献5更容易理解,这里 把他的图贴出来,实际过程就不再重复赘述了。
两个参谋先后提议的场景:
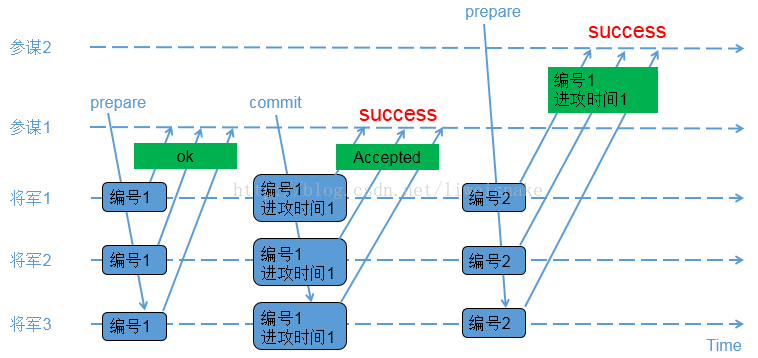
两个参谋交叉提议的场景:

需要注意的是参谋1在失败时再次发起请求的过程。
这里着重强调几个重点。
1. 算法描述里有好几个地方要求投票必须超过半数,这个超过半数恰恰是保证一致的一个必要条件
2. 算法里也有多处要求只选择编号最大的,这种选择编号最大的方式,是一种最为简单经济的达成共识的方法,能够快速在多个冲突中找到一个突破口
3. paxos算法的关键是,如果一个值m被选中了,那么必须保证更高的proposal其值也为m
4. 注意第一阶段比较的是已经批准过的proposal的最大编号,而第二阶段比较的是prepare请求。即第一阶段比较的是第二阶段的结果,而第二阶段比较的是第一阶段的结果,看似很绕,实际上正好是隔离了阶段外的保证,进入第一阶段的我要保证他是新的开始,跟上一阶段没啥关系,而进入第二阶段的我要保证他是从前面阶段来的,而不是新起的一个阶段,有点像是隔离锁,锁住了阶段一到阶段二这个过程。
Zookeeper默认采用FastLeaderElection算法,然而FastLeaderElection对于Zookeeper来讲只是相当于paxos中的leader选举。
下面我用最简单的方式加以描述并建立起Paxos和ZKServer的对应关系。
Paxos描述了这样一个场景:
1、有一个叫做Paxos的小岛(Island)上面住了一批居民,岛上面所有的事情由一些特殊的人决定,他们叫做议员(Senator)。
2、议员的总数(SenatorCount)是确定的,不能更改。 3、岛上每次环境事务的变更都需要通过一个提议(Proposal),每个提议都有一个编号(PID),这个编号是一直增长的,不能倒退。 4、每个提议都需要超过半数((SenatorCount)/2+1)的议员同意才能生效。 5、每个议员只会同意大于当前编号的提议,包括已生效的和未生效的。 6、如果议员收到小于等于当前编号的提议,他会拒绝,并告知对方:你的提议已经有人提过了。这里的当前编号是每个议员在自己记事本上面记录的编号,他不断更新这个编号。整个议会不能保证所有议员记事本上的编号总是相同的。
现在议会有一个目标:保证所有的议员对于提议都能达成一致的看法。
好,现在议会开始运作,所有议员一开始记事本上面记录的编号都是0。
有一个议员发了一个提议: 将电费设定为1元/度。他首先看了一下记事本,嗯,当前提议编号是0,那么我的这个提议的编号就是1,于是他给所有议员发消息:1号提议,设定电费1元/度。其他议员收到消息以后查了一下记事本,哦,当前提议编号是0,这个提议可接受,于是他记录下这个提议并回复:我接受你的1号提议,同时他在记事本上记录:当前提议编号为1。发起提议的议员收到了超过半数的回复,立即给所有人发通知:1号提议生效!收到的议员会修改他的记事本,将1好提议由记录改成正式的法令,当有人问他电费为多少时,他会查看法令并告诉对方:1元/度。现在看冲突的解决:
假设总共有三个议员S1-S3,S1和S2同时发起了一个提议:1号提议,设定电费。S1想设为1元/度,S2想设为2元/度。结果S3先收到了S1的提议,于是他做了和前面同样的操作。紧接着他又收到了S2的提议,结果他一查记事本,咦,这个提议的编号小于等于我的当前编号1,于是他拒绝了这个提议:对不起,这个提议先前提过了。于是S2的提议被拒绝,S1正式发布了提议:1号提议生效。S2向S1或者S3打听并更新了1号法令的内容,然后他可以选择继续发起2号提议。
好,我觉得Paxos的精华就这么多内容。现在让我们来对号入座,看看在ZKServer里面Paxos是如何得以贯彻实施的。 小岛(Island)——ZKServerCluster 议员(Senator)——ZKServer 提议(Proposal)——ZNodeChange(Create/Delete/SetData…) 提议编号(PID)——Zxid(ZooKeeperTransactionId) 正式法令——所有ZNode及其数据: 貌似关键的概念都能一一对应上,但是等一下,Paxos岛上的议员应该是人人平等的吧,而ZKServer好像有一个Leader的概念。没错,其实Leader的概念也应该属于Paxos范畴的。如果议员人人平等,在某种情况下会由于提议的冲突而产生一个“活锁”(所谓活锁我的理解是大家都没有死,都在动,但是一直解决不了冲突问题)。Paxos的作者Lamport在他的文章”ThePart-TimeParliament“中阐述了这个问题并给出了解决方案——在所有议员中设立一个总统,只有总统有权发出提议,如果议员有自己的提议,必须发给总统并由总统来提出。好,我们又多了一个角色:总统。 总统——ZKServerLeader
又一个问题产生了,总统怎么选出来的?
现在我们假设总统已经选好了,下面看看ZKServer是怎么实施的。
情况一:
屁民甲(Client)到某个议员(ZKServer)那里询问(Get)某条法令的情况(ZNode的数据),议员毫不犹豫的拿出他的记事本(localstorage),查阅法令并告诉他结果,同时声明:我的数据不一定是最新的。你想要最新的数据?没问题,等着,等我找总统Sync一下再告诉你。 情况二: 屁民乙(Client)到某个议员(ZKServer)那里要求政府归还欠他的一万元钱,议员让他在办公室等着,自己将问题反映给了总统,总统询问所有议员的意见,多数议员表示欠屁民的钱一定要还,于是总统发表声明,从国库中拿出一万元还债,国库总资产由100万变成99万。屁民乙拿到钱回去了(Client函数返回)。 情况三: 总统突然挂了,议员接二连三的发现联系不上总统,于是各自发表声明,推选新的总统,总统大选期间政府停业,拒绝屁民的请求。 呵呵,到此为止吧,当然还有很多其他的情况,但这些情况总是能在Paxos的算法中找到原型并加以解决。这也正是我们认为Paxos是Zookeeper的灵魂的原因。当然ZKServer还有很多属于自己特性的东西:Session,Watcher,Version等等,需要我们花更多的时间去研究和学习。